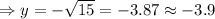Question

Point A has an x-coordinate of 7 and lies below the x-axis on a circle with a center at (0, 0) and a radius of 8. To the nearest tenth, what is the y-coordinate for point A? −4.0 −3.9 −3.8 −3.7

Answer 1

The y-coordinate for point is -3.9

Solution-

Point A has an x-coordinate of 7 and lies below the x-axis (i.e -ve y-coordinate)

Let us assume, the coordinates of the point is (7, y)

The general equation for circle with centre at (h, k) and radius r, is

`\Rightarrow (x-h)^2+(y-k)^2=r^2`

As here the centre is origin (0, 0) and radius 8, so equation of the circle is

`\Rightarrow x^2+y^2=8^2`

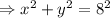
As point A lies on the circle, so it must satisfy the circle equation, so

`\Rightarrow 7^2+y^2=8^2`

`\Rightarrow y^2=8^2-7^2=64-49=15`

`\Rightarrow y=\pm √(15)`

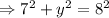
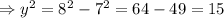
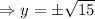
As the point lies under x axis, so considering only -ve value,

`\Rightarrow y=-√(15)=-3.87\approx -3.9`

Answer 2

the formula of a circle is: x2 + y2 = r2

substituting known values in the formula: x=7 and r=8

72 + y2 = 82

calculating for value of y:

y2=64-49

y=±√15

y=±3.9

since point A lies below the x-axis then

y=-3.9