Answer:
Option d - 7, 13, 19, 25, 31, 37
Explanation:
Given :
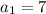 and
and
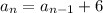
To find : The first six terms of the sequence?
Solution :
We have given the nth formula,
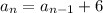
The first term is
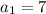
For second term put n=2,
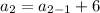
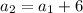
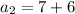
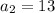
For third term put n=3,
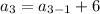
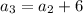
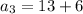
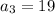
For fourth term put n=4,
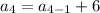
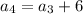
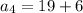
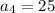
For fifth term put n=5,
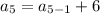
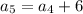
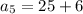
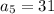
For sixth term put n=6,
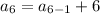
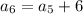
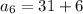
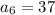
Therefore, The required sequence is 7, 13, 19, 25, 31, 37.
So, Option d is correct.