Question

What is the measure of angle A to the nearest degree

Answer 1

sin A = 56/75
A = sin^-1 (56/75) = 48.30 degrees

Answer 2

`A\approx 48^o`

Explanation:

We have been given an image of a right triangle and we are asked to find the measure of angle A of our given triangle.

We can see that hypotenuse and opposite side to angle A is given. Since sine represents the relation between opposite and hypotenuse of a right triangle, so we will use sine to find the measure of angle A.

`\text{Sin}=\frac{\text{Opposite}}{\text{Hypotenuse}}`

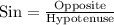
Upon substituting our given values in above relation we will get,

`\text{Sin A}=(56)/(75)`

`A=\text{Sin}^(-1)((56)/(75))`

`A=48.302453396837^o`

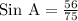
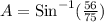
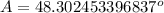
Upon rounding our answer to nearest degree we will get,

`A\approx 48^o`

Therefore, the measure of angle A to the nearest degree is 48 degrees.