Question

Which expression is equivalent to 3/343x^9v^12z^6 ?

A) 7x3y4z2
B) 7x3y6z2
C) 49x3y6z2
D) 49x3y4z2

Answer 1

I assume you mean the cube root of the variable,
which is (x^3 v^4 z^2)

Answer 2

Option a

Explanation:

Given is an expression

`343x^9v^(12)  z^6`

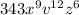
We have to find the cube root of this expression.

This is product of constant and 3 variables.

So let us find cube root for each separately and multiply at last to get the answer.

`\sqrt[3]{343} =7\\\sqrt[3]{x^9} =x^3\\\sqrt[3]{v^(12) } =v^4\\\sqrt[3]{z^6} =z^2`

Thus cube root of given expression = product of these four

=
`7x^3v^4z^2`

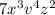
Option a is right