Question

What are the critical points for the inequality x^2 - 4/x^2 - 5x +6 < 0?

a. x = –2 and x = 2
b. x = 2 and x = 3
c. x = –3, x = –2, and x = 2
d. x = –2, x = 2, and x = 3

Answer 1

Critical points are: 2 , -2 and 3.

Explanation:

We have been given the expression:

`(x^2-4)/(x^2-5x+6)<0`

We will factorize the given expression:

Using
`a^2-b^2=(a+b)(a-b)`

`((x+2)(x-2))/(x^2-3x-2x+6)<0`

`\Rightarrow ((x+2)(x-2))/(x(x-3)-2(x-3))<0`

`\Rightarrow ((x+2)(x-2))/((x-2)(x+3))<0`

Critical point are those values of an expression when it is equal to zero

Hence, the critical points are: 2,-2 and -3.

Answer 2

d. x = –2, x = 2, and x = 3 are critical points.

Explanation:

Given :
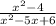`(x^(2)-4 )/(x^(2)-5x+6)` < 0.

To find :What are the critical points for the inequality.

Solution : We have given that

`(x^(2)-4 )/(x^(2)-5x+6)` < 0.

Using
`a^(2)-b^(2) = (a+b)(a-b)`

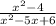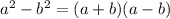
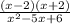`((x-2)(x+2) )/(x^(2)-5x+6)` < 0.

Now, on factoring denominator

`x^(2) -5x+6`

`x^(2) -3x -2x+6`

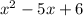
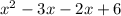
Taking commom

x( x- 3) -2(x -3)

On grouping (x-3)(x -2)

`((x-2)(x+2) )/((x-3)(x-2))<0` .

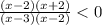We need to find critical point ,

Critical point on which expression is zero

Then x = 2, -2, 3 are critical point.

Therefore, d. x = –2, x = 2, and x = 3 are critical points.