Answer:
d. x = –2, x = 2, and x = 3 are critical points.
Explanation:
Given :
 < 0.
< 0.
To find :What are the critical points for the inequality.
Solution : We have given that
 < 0.
< 0.
Using
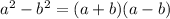
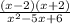 < 0.
< 0.
Now, on factoring denominator

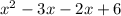
Taking commom
x( x- 3) -2(x -3)
On grouping (x-3)(x -2)
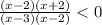 .
.
We need to find critical point ,
Critical point on which expression is zero
Then x = 2, -2, 3 are critical point.
Therefore, d. x = –2, x = 2, and x = 3 are critical points.