When you roll a number cube, there is a possibility of a number from 1 to 6 appearing. i.e. 1, 2, 3, 4, 5, or 6 can appear.
The same goes for the second number cube.
The table below presents the possible outcomes of rolling two number cubes with the sum written as exponent.
![\begin{center} \begin{tabular} c & 1 & 2 & 3 & 4 & 5 & 6 \\ [1ex] 1 & \{1,1\}^2 & \{1,2\}^3 & \{1,3\}^4 & \{1,4\}^5 & \{1,5\}^6 & \{1,6\}^7 \\ 2 & \{2,1\}^3 & \{2,2\}^4 & \{2,3\}^5 & \{2,4\}^6 & \{2,5\}^7 & \{2,6\}^8 \\ 3& \{3,1\}^4 & \{3,2\}^5 & \{3,3\}^6 & \{3,4\}^7 & \{3,5\}^8 & \{3,6\}^9 \\ 4 & \{4,1\}^5 & \{4,2\}^6 & \{4,3\}^7 & \{4,4\}^8 & \{4,5\}^9 & \{4,6\}^(10) \\ \end{tabular} \end{center}](https://img.qammunity.org/2018/formulas/mathematics/high-school/7gittrnhywlyuv0wmxrm17eme1odd8hb63.png)
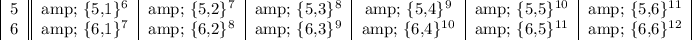
From the table it can be seen that the sums: 2 and 12 appeared only once and hence will represent the shortest bars if the distribution is represented in a bar chart.
Therefore, the
two sums that are represented by the shortest bars on a bar graph of this distribution are 2 and 12.