Question

A ball is thrown in the air from a ledge. Its height in feet is represented by

f(x) = –16(x2 – 6x – 7), where x is the number of seconds since the ball has been thrown. The height of the ball is 0 feet when it hits the ground.

How many seconds does it take the ball to reach the ground?

Answer 1

It takes the ball 7 seconds to reach the ground.

Answer 2

The time taken by the ball to reach the ground is 7 seconds.

Explanation:

Given : A ball is thrown in the air from a ledge. Its height in feet is represented by
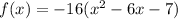`f(x) = -16(x^2-6x-7)`, where x is the number of seconds since the ball has been thrown. The height of the ball is 0 feet when it hits the ground.

To find : How many seconds does it take the ball to reach the ground?

Solution :

The function

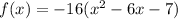`f(x) = -16(x^2-6x-7)` represent the height of the ball.

Where, x is the number of seconds.

We have given that the height of the ball is 0 feet when it hits the ground

and we to find the seconds does it take the ball to reach the ground.

i.e., we have to take f(x)=0 and find x.

`0= -16(x^2-6x-7)`

`x^2-6x-7=0`

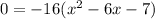
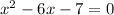
Applying middle term split,

`x^2-7x+x-7=0`

`x(x-7)+1(x-7)=0`

`(x-7)(x+1)=0`

`x=7,-1`

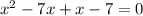
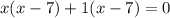
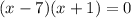
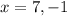
x=-1 is rejected as time is not negative.

x=7 is accepted.

Therefore, The time taken by the ball to reach the ground is 7 seconds.