Answer:
The range of f(x) is
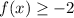 and option D is correct.
and option D is correct.
Explanation:
The given function is
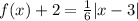
It can be written as
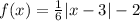 .... (1)
.... (1)
The function is in the form of
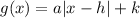 ....(2)
....(2)
Where, a is scale factor and (h,k) is vertex of the graph.
On comparing (1) and (2), we get
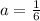
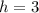
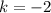
Therefore the vertex of f(x) is (3,-2). Option A is incorrect.
The value of a is
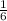 . So, the graph compressed vertically. The value of a is positive, therefore the graph of f(x) opens upward.
. So, the graph compressed vertically. The value of a is positive, therefore the graph of f(x) opens upward.
We know the absolute value is always greater than or equal to 0.
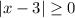
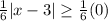
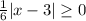
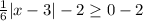
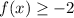
Therefore the range of f(x) is
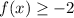 and option D is correct.
and option D is correct.