Which statement is true about f(x)+2=1/6|x-3|? A. The graph of f(x) has a vertex of (-3,2). B. The graph of f(x) is horizontally compressed. C. The graph of f(x) opens downward.…

Question

asked Oct 25, 2018 216k views

2 Answers

Maf · Answer 1 · 2018-11-01T15:49:46+0000

Answer:

The range of f(x) is
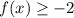$f(x)\geq -2$ and option D is correct.

Explanation:

The given function is

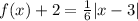
f(x)+2=(1)/(6)|x-3|

It can be written as

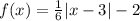f(x)=(1)/(6)|x-3|-2 .... (1)

The function is in the form of

g(x)=a|x-h|+k ....(2)

Where, a is scale factor and (h,k) is vertex of the graph.

On comparing (1) and (2), we get

a=(1)/(6)

h=3

k=-2

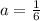
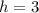
Therefore the vertex of f(x) is (3,-2). Option A is incorrect.

The value of a is
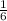(1)/(6) . So, the graph compressed vertically. The value of a is positive, therefore the graph of f(x) opens upward.

We know the absolute value is always greater than or equal to 0.

$|x-3|\geq 0$

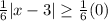
$(1)/(6)|x-3|\geq (1)/(6)(0)$

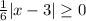
$(1)/(6)|x-3|\geq 0$

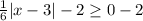
$(1)/(6)|x-3|-2\geq 0-2$

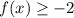
$f(x)\geq -2$

Therefore the range of f(x) is
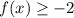$f(x)\geq -2$ and option D is correct.