Question

Which is the equation of a parabola with vertex (0, 0), that opens to the left and has a focal width of 12?

Answer 1

Answer: B

Equation of parabola is y^2=-12x

Answer 2

`\text{Equation of parabola is }y^2=-12x`

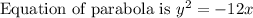
Explanation:

We need to find the equation of parabola using given information

• Vertex: (0,0)
• Open to the left
• Focal width = 12

If parabola open left and passes through origin then equation is

`y^2=-4ax`

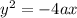
Focal width = 12

Focal width passes through focus and focus is mid point of focal width.

Focus of above parabola would be (-a,0)

Passing point on parabola (-a,6) and (-a,-6)

Now we put passing point into equation and solve for a

`6^2=-4a(-a)`

`a=\pm 3`

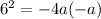
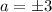
a can't be negative.

Therefore, a=3

Focus: (-3,0)

Equation of parabola:

`y^2=-12x`

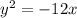
Please see the attachment of parabola.

`\text{Thus, Equation of parabola is }y^2=-12x`