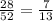Answer:
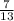
Explanation:
Total number of cards in deck of playing cards = 52
Number of ace in deck of playing cards i.e n(P)= 4
Number of red cards in deck of playing cards i,e n(Q) =
Number of diamonds + Number of hearts = 13+ 13 = 26
Number of ace which are red cards i,e
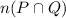 = 2
= 2
To Find:
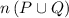
Solution:
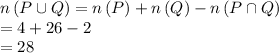
So, probability that the card drawn is an ace or a red card =
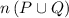 /Total number of cards
/Total number of cards
=