Answer:
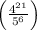
or
4 to the 21st over 5 to the 6th.
Explanation:
First, we need to write our expression. Let's do it step by step:
4 to the 7th:
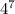
5 squared:
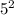
4 to the 7th over 5 squared:
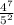
4 to the 7th over 5 squared all raised to the 3rd power:
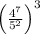
Using the law of exponents:
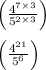
Finally, the answer is 4 to the 21st over 5 to the 6th.