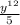Answer:
An equivalent expression to the given expression
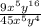 is
is
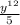
Explanation:
Given : Expression
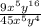
We have to find an equivalent expression to the given expression
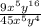
Consider the given expression
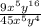
Cancel the common factor 9, we have,
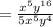
Cancel the common factor
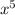 , we have,
, we have,
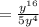
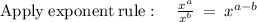
We have,
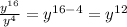
Thus, we get,
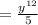
Thus, An equivalent expression to the given expression
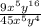 is
is