Answer: The required present age of Ralph is 12 years.
Step-by-step explanation: Given that Ralph is 3 times as old as Sara and in 4 years, Ralph will be only twice as old as Sara will be then.
We are to find the present age of Ralph.
Let r and s represents the present ages of Ralph and Sara respectively.
According to the given information, we have

Substituting the value of r from equation (i) in equation (ii), we get
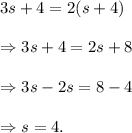
Therefore, from equation (i), we get
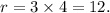
Thus, the required present age of Ralph is 12 years.