Answer:
2feet and 8 feet.
Explanation:
Let's call L to the length of the garden. Now, we have that the height h is
h = 6+L and the area of a triangle is
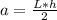 . Then:
. Then:
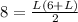
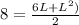
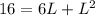

we are going to use cuadratic formula to find L.
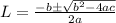 where a= 1, b=6 and c=-16. Then,
where a= 1, b=6 and c=-16. Then,
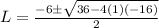
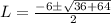
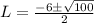
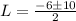
So, L = 4/2 = 2 or L = -16/2 = -8 but as we are searching lengths, we use the positive result. Then L = 2. Finally we have that the length of the triangle is 2 feet and the height is 2+6 = 8 feet.