Question

How many x intercepts appear on the graph of this polynomial function? f(x)=x^4-5x^2

Answer 1

The function can be factorised to give x²(x²-5). Therefore the graph will touch the x axis at zero and cut it at -√5 and √5, giving three x-intercepts. To check, let's look at a graph my calculator drew of this function:

Answer 2

From the diagram you can see that the graph of function has three x-intercepts. If you need the coordinates of these points, then you should substitute y=0 and solve the received equation:

`0=x^4-5x^2`.

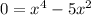First, factor this expression:

`x^2(x^2-5)=0,\\x^2(x-√(5)) (x+√(5))=0`.

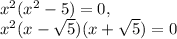This means that

`x_1=0, x_2=√(5) ,x_3=-√(5)`.

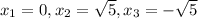The x-intercepts are points

`(0,0), (√(5),0), (-√(5),0)`.

Answer: 3 x-intercepts.