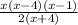In order to solve the product of polynomials simplify the numerator and denominator following those steps
we have
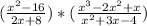
Step 1
Using difference of squares and complete squares in the numerator
![({x^(2)-16})*({x^(3)-2x^(2)+x)=[(x+4)(x-4)]*[x(x^(2)-2x+1)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/atm777odbm3k3906y0yevqxtydiiv82zh4.png)
![[(x+4)(x-4)]*[x(x^(2)-2x+1)]=[(x+4)(x-4)]*[x(x-1)^(2)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/mb6s631ctiq8of0yb0ls42u2v2jifvrbgs.png)
Step 2
Complete squares in the denominator
![(2x+8)*(x^(2)+3x-4)=[2(x+4)]*[(x+4)(x-1)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/pa1plme16zljrb11yxmnaxc5g141nq84zb.png)
Step 3
Substitute
![([(x+4)(x-4)]*[x(x-1)^(2)])/([2(x+4)]*[(x+4)(x-1)])](https://img.qammunity.org/2018/formulas/mathematics/high-school/hh6gsdog7jhz6ou3zbo8jdhj7m8wia8ls5.png)
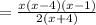
therefore
the answer is the option A