Answer:
Given the system of equation:
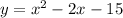 .....[1]
.....[1]
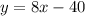 ......[2]
......[2]
Equate these two equations we get;
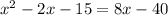
Subtract 8x to both sides we have;
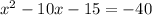
Add 40 to both sides we have;
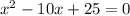
Using the identity rule:
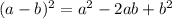
then;

⇒
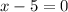
Add 5 to both sides we have;
x = 5
Substitute this value in [2] we have;
y=8(5)-40 = 40-40 = 0
therefore, the solution(s) of the system of equations is, (5, 0)