Answer:
The answer is 1
Explanation:
In order to complete the square, you have to know the rule for expanding a square of a binomial.
The rule says:
Let
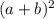 a square of a binomial in general
a square of a binomial in general
The square of any binomial produces the following three terms:
1. The square of the first term of the binomial:
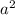
2. Twice the product of the two terms:

3. The square of the second term:
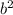
So, the expand of a square of a binomial is:
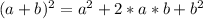
Therefore, we should think which of the three terms mentioned before it is absent.
1. First term is
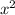
2. Second term is

3. Third term must be
 because it is the unique number which multiplying by
because it is the unique number which multiplying by
 results in
results in

Finally, adding 1 in both side of the equation:
