Question

Which equation is y = –3x2 – 12x – 2 rewritten in vertex form?

Answer 1

y=-6-12x-2
y=-6-12x-2
y=-8-12x
y=-8-12x
and these are real numbers

Answer 2

The vertex form of the given equation is
`y=-3(x+2)^2+10`.

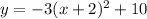Explanation:

The vertex form of a parabola is

`y=a(x-h)^2+k`.

The given equation is

`y=-3x^2-12x-2`

`y=(-3x^2-12x)-2`

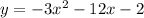
Take the common coefficients.

`y=-3(x^2+4x)-2`

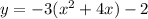
If an expression is defined as
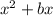`x^2+bx`, then we need to add
`((b)/(2))^2` to make it perfect square.

Here b=4, so we need to add
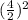`((4)/(2))^2` in the parenthesis.

`y=-3(x^2+4x+2^2-2^2)-2`

`y=-3(x^2+4x+2^2)-3(-2^2)-2`

`y=-3(x+2)^2-3(-4)-2`

`y=-3(x+2)^2+12-2`

`y=-3(x+2)^2+10`

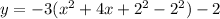
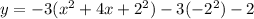
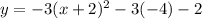
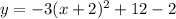
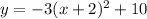
Therefore the vertex form of the given equation is
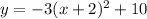`y=-3(x+2)^2+10`.