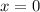Question

Which is the axis of symmetry of a parabola with equation x^2=-4y?

x = –4
x = –1
x = 0
x = 1

Answer 1

y=a(x-h)²+k

x=h is the axis of symmetry
so
-4y=x²
times both sides by -1/4
y=(-1/4)x²
y=(-1/4)(x-0)²+0
axis of symmetry is x=0

3rd option

Answer 2

The axis of symmetry is
`x=0`

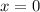
Explanation:

we know that

The equation of a vertical parabola into vertex form is equal to

`y=a(x-h)^(2) +k`

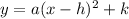
where

(h,k) is the vertex of the parabola

and the axis of symmetry is the x-coordinate of the vertex

`x=h`

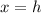
In this problem we have

`x^(2) =-4y`

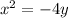
The vertex is the origin

therefore

the axis of symmetry is

`x=0`