Question

The lengths of two sides of a right triangle are given. Find the length of the third side. Round to the nearest tenth if necessary.

legs: 28 in. and 15 in.

Answer 1

Since it's a right triangle, the Pythagorean theorem can be used to find the thrid side.

Pythagorean's Theorem states that
`a^(2)~+~b ^(2)= c^(2)` where a and b are the measure of the legs.

So it's going to be
`28^(2) + 15 ^(2) =c ^(2)`.
784 + 225 =
`c^(2)`
1009 =
`c^(2)`
c = 31.76

So the length of the third side is 31.76 inches

Answer 2

31.76 in.

Explanation:

The problem states that the triangle is a right triangle, meaning, one of its internal angles measures 90° (see the attached image).

Since it's a right triangle, the Pythagorean's theorem can be used to find the third side, where a=28 inches and b=15 inches.

The Pythagorean's Theorem states:

`c^(2) = a^(2) +b^(2)`

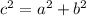
Changing a and b in the above formula for it's respective values, we have:

`c^(2) = 28^(2)  +15^(2)`

`c^(2) = 784 + 225`

`c=√(784+225)`

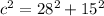
c=31.76