Answer:
22.05 meters
Step-by-step explanation:
In order to get the answer, basically it is a distance we are looking for.
We are going to get familiar with the formula of displacement:
Δx
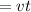
![v[/text]= <strong>average velocity</strong></p><p>[tex]t[/text]= <strong>time in motion</strong></p><p>Because it is a projectile in motion thrown at a 29.4 m/s with an angle of 30°, we need to find the <u><em>vertical</em></u><u> </u>part of that velocity. </p><p></p><p>The <em>vertical </em>part is given by the [tex]sin]() of the angle of 30°
of the angle of 30°
that is
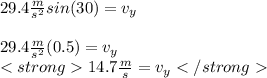 average velocity
average velocity
Now
Δ
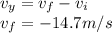 \\ because the baseball goes the opposite direction when is going down until it gets to the grown. Then
\\ because the baseball goes the opposite direction when is going down until it gets to the grown. Then
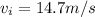
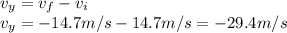
and using this formula
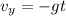
we divide both sides by
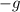 and we get
and we get
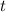
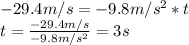
Finally 3 seconds is the time in motion, so we divide by two because we just need the time going up, that happens to be the same time going down.
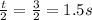 time in motion
time in motion
Δx
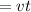
![v[/text]= <strong>average velocity=[tex]14.7(m)/(s)](https://img.qammunity.org/2018/formulas/physics/high-school/2syfzgwy04j27ihwiv8saj283ywjbz69m3.png)
![t[/text]= <strong>time in motion=[tex]1.5s](https://img.qammunity.org/2018/formulas/physics/high-school/ac8fxl32ds7z1m8u4x6mm77vjmnq86m8ai.png)
