Answer:
Option B is correct.
Explanation:
Given that

and the terminal point
 is in quadrant 2,i.e
is in quadrant 2,i.e
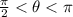
we have to find the value of
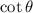
As in second quadrant
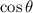 is negative.
is negative.
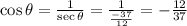
As in second quadrant all trigonometric functions are negative except
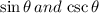
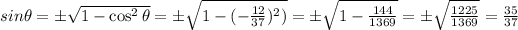
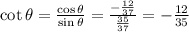
Option B is correct.