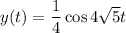Question

A spring has natural length 0.75 m and a 5 kg mass. A force of 8 N is needed to keep the spring stretched to a length of 0.85 m. If the spring is stretched to a length of 1 m and then released with velocity 0, find the position of the mass after t seconds.

Answer 1

Use Hooke's law to find the spring constant. If it takes 8N to stretch the spring by 0.1m, then


`8\text{ N}=k(0.1\text{ m})\implies k=80(\text N)/(\text m)`

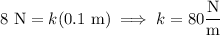
I'm going to assume the spring is fixed to a ceiling, and that any stretching in the downward direction counts as movement in the positive direction. The spring's motion is then modeled by


`y''(t)+80y(t)=0`

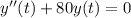
where
`y(t)` is the position of the spring's free end as it moves up and down. Solving this is easy enough: the characteristic solution will be


`y(t)=C_1\cos4\sqrt5t+C_2\sin4\sqrt5t`

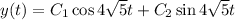
Given that the spring is stretched to a length of 1m (a difference of 0.25m from its natural length), and is released with no external pushing or pulling, we have the two initial conditions
`y(0)=\frac14` and
`y'(0)=0`.


`y(0)=\frac14\implies\frac14=C_1\cos0+C_2\sin0\implies C_1=\frac14`

`y'(0)=0\implies 0=-4\sqrt5C_1\sin0+4\sqrt5C_2\cos0\implies C_2=0`

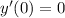
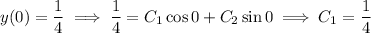
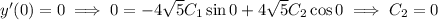
So the spring's motion is dictated by the function


`y(t)=\frac14\cos4\sqrt5t`