Question

Rewrite x^3+5x^2+3x-10/x+4 in the form q(x)+r(x)/b(x)

Answer 1

One way to do it: Find coefficients
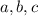
`a,b,c` such that


`x^3+5x^2+3x-10=(x+4)^3+a(x+4)^2+b(x+4)+c`

`=x^3+(a+12)x^2+(8a+b+48)x+(16a+4b+c+64)`

`\implies\begin{cases}5=a+12\\3=8a+b+48\\-10=16a+4b+c+64\end{cases}\implies a=-7,b=11,c=-6`

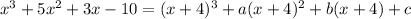
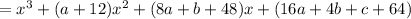
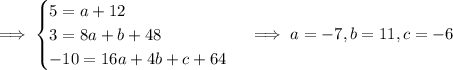
So, we have


`(x^3+5x^2+3x-10)/(x+4)=((x+4)^3-7(x+4)^2+11(x+4)-6)/(x+4)`

`=(x+4)^2-7(x+4)+11-\frac6{x+4}`

`=x^2+x-1-\frac6{x+4}`

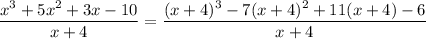
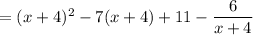
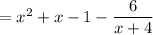
This can also be done with long or synthetic division. Just to verify the result above, synthetic division yields

-4 | 1 5 3 -10
. | -4 -4 4
- - - - - - - - - - - - - -
. | 1 1 -1 -6

which translates to


`(x^3+5x^2+3x-10)/(x+4)=x^2+x-1-\frac6{x+4}`

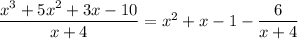
as required.

Here,
`q(x)=x^2+x-1`,
`r(x)=-6`, and
`b(x)=x+4`.