Question

For what value of C will y = sin(x - C) be an even function?
a. 2π
b. π
c. π/2

Answer 1

you are actually incorrect the answer is 2π

Answer 2

c.
`(\pi)/(2)`

Explanation:

We are given that

`y=sin(x-C)`

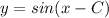
We have to find the value of C for which given function is even function.

We know that

Even function : If f(x)=f(-x) then the function is called even function.

`a.2\pi`

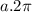
Substitute the value then we get

`y= sin(x-2\pi)= sin(-(2\pi-x))=-sin (2\pi-x)=sin x`

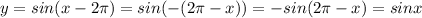
We know that sin (-x)=-sin x,
`sin(2\pi-x)=-sinx`

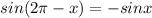
We know that Sin x is an odd function , therefore, option a is incorrect.

b.
`\pi`

Substitute the value then we get

`y= sin (x-\pi)=sin(-(\pi-x))=-sin (\pi-x)=-sin x`

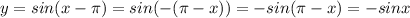
It is an odd function.

Hence, option b is incorrect.

c.
`(\pi)/(2)`

Substitute the value then we get

`y= sin(x-(\pi)/(2))=sin(-((\pi)/(2)-x))=-sin((\pi)/(2)-x)=-cos x`

`sin((\pi)/(2)-x)=cosx`

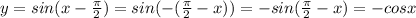
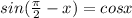
We know that cos x is even function

Replace x by -x then, we get

`-cos (-x)=-cos x`....(cos (-x)=cos x)

Hence, the value of C=
`(\pi)/(2)` for which given function will be an even function.

Answer:c.
`(\pi)/(2)`