Answer:
The required matching is a-1, b-4, c-3, d-5, e-2, f-6.
Explanation:
Unit Circle is circle having radius 1 units and centered at origin.
The terminal side intersects the Unit Circle at the point (x, y), and neither x nor y is equal to zero.
So, perpendicular of triangle is y, base is x and hypotenuse is 1 unit.
It a right angled triangle,

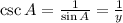
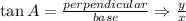
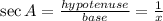
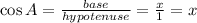
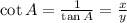
Therefore the required matching is a-1, b-4, c-3, d-5, e-2, f-6.