Question

The following two sets of parametric functions both represent the same ellipse. Explain the difference between the graphs.

x = 3 cos t and y = 8 sin t
x = 3 cos 4t and y = 8 sin 4t

Answer 1

the answer
ellipse main equatin is as follow:

X²/ a² + Y²/ b² =1, where a≠0 and b≠0

for the first equation: x = 3 cos t and y = 8 sin t
we can write x² = 3² cos² t and y² = 8² sin² t
and then x² /3²= cos² t and y²/8² = sin² t
therefore, x² /3²+ y²/8² = cos² t + sin² t = 1
equivalent to x² /3²+ y²/8² = 1

for the second equation, x = 3 cos 4t and y = 8 sin 4t we found
x² /3²+ y²/8² = cos² 4t + sin² 4t=1

Answer 2

Answer with explanation:

The two parametric equation of the same ellipse is

x = 3 cos t and y = 8 sin t

x = 3 cos 4 t and y = 8 sin 4 t

`(x)/(3)=\cos t\\\\ (x)/(3)=\cos 4t\\\\ (y)/(8)=\sin t\\\\ (y)/(8)=\sin 4t\\\\ ((x)/(3))^2+ ((y)/(8))^2=\sin^2t+\cos^2t \text{or}=\sin^2 4t+\cos^2 4t=1\\\\(x^2)/(9)+(y^2)/(64)=1`

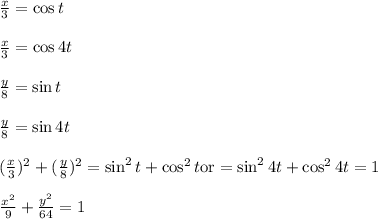
This is the equation of same ellipse, having different Parametric forms.

→The function involving , 3 cos t and 8 sin t has maximum value, 3 and 8,respectively , and a period of π , whereas, the function 3 cos 4 t and , 8 sin 4 t , has also same maximum value, 3 and 8,respectively , but period changes , the period after which cycle of trigonometric function sin 4 t and cos 4 t repeats is,
`t=(\pi)/(4)`.

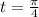→x = 3 cos t and y = 8 sin t

`(x)/(y)=(3)/(8 \tan t)\\\\y=(8 \tan t*x)/(3)`

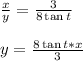
→x = 3 cos 4 t and y = 8 sin 4 t

`(x)/(y)=(3)/(8 \tan 4 t)\\\\y=(8 \tan 4 t*x)/(3)`

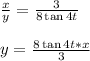
Also, these are equation of two lines having different slopes both passing through the origin.