Answer:
126 ways.
Explanation:
Since the order does not matter, the solution is obtained through a combination where we choose "r of n", where r is the amount of things we choose and n the total number of things that can be chosen.
In the given case,
r = 4
n = 9
The combinations form uses factorial numbers. This is the formula:
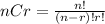
The factorial function (symbol:!) means that descending numbers are multiplied to 1.
We substitute the values in the equation and get

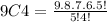
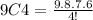
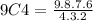
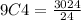
9C4 = 126
Therefore, there are 126 ways to choose a committee of 4 from a group of 9 people.
Hope this helps!