Answer:
The sequence is:
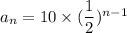
and the average rate of change from n=0 to n=2 is:
-7.5
Explanation:
We are given the points as:
(1,10), (2,5) and (4,1.25)
Clearly after looking the point we see that these point follow a geometric sequence.
Since with the increase in x-value by 1 unit there is a decrease in the y-value by a factor of 1/2
Let the points be denoted by:
Hence, we have the sequence as:
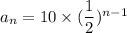
Since, when x=n=1 we have:
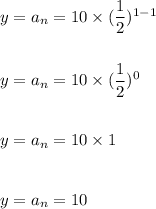
Similarly we can check the other points as well
When x=n=0
we have:
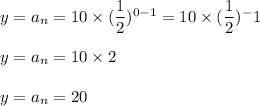
Now, the average rate of change from n=0 to n=2 is calculated as:
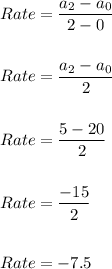
Hence, Rate= -7.5