Question

Identify the sequence graphed below and the average rate of change from n = 0 to n = 2.

coordinate plane showing the point 1, 10, point 2, 5, and point 4, 1.25

Answer 1

We must find the equation of this function first. This is a geometric sequence as each term is a constant ratio of the previous term...

5/10=1/2, And this sequence can be expressed as:

a(n)=10(1/2)^(n-1) So the term when n=0 would be 20

The average rate of change is just the change in y divided by the change in x, in this case:

(20-5)/(2-0)

7.5

Answer 2

The sequence is:

`a_n=10* ((1)/(2))^(n-1)`

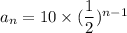
and the average rate of change from n=0 to n=2 is:

-7.5

Explanation:

We are given the points as:

(1,10), (2,5) and (4,1.25)

Clearly after looking the point we see that these point follow a geometric sequence.

Since with the increase in x-value by 1 unit there is a decrease in the y-value by a factor of 1/2

Let the points be denoted by:
`(n,a_n)`

Hence, we have the sequence as:

`a_n=10* ((1)/(2))^(n-1)`

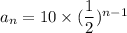
Since, when x=n=1 we have:

`y=a_n=10* ((1)/(2))^(1-1)\\\\\\y=a_n=10* ((1)/(2))^(0)\\\\\\y=a_n=10* 1\\\\\\y=a_n=10`

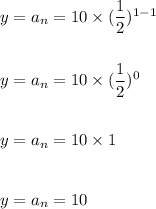
Similarly we can check the other points as well

When x=n=0

we have:

`y=a_n=10* ((1)/(2))^(0-1)=10* ((1)/(2))^-1\\\\y=a_n=10* 2\\\\y=a_n=20`

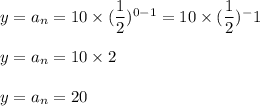
Now, the average rate of change from n=0 to n=2 is calculated as:

`Rate=(a_2-a_0)/(2-0)\\\\\\Rate=(a_2-a_0)/(2)\\\\\\Rate=(5-20)/(2)\\\\\\Rate=(-15)/(2)\\\\\\Rate=-7.5`

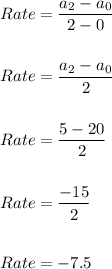
Hence, Rate= -7.5