Question

Compute the permutation.

How many positive integers of 3 digits each can be formed with the digits 1, 8, 9, 2, 7, 6, 4, and 3, if no digit is repeated in a number?

Answers:
27,
336,
512

Answer 1

336

Explanation:

Answer 2

So you have 8 digits (number available) to form 3 digit numbers (number selected).

Using the formula
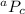
`^(a) P_(c)` where a is the number of available digits, P is the permutation function and c is the number of digits to be selected.

The number of three digit numbers that can be formed =
`^(8) P_(3)`
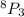
= 336

O R

By using the formula
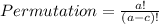`Permutation = (a ! )/(( a - c) !)` where a is the number of available digits and c is the number of digits to be selected.

⇒
`Permutation = (8 ! )/(( 8 - 3) !)`

⇒
`Permutation = (40, 320 )/(120)`

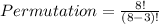
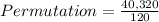
⇒ Permutation = 336