Answer:
x= -5
Explanation:
we are given with the function:
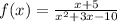
We will factorize the denominator
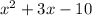
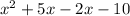


Hence, We can see that (x+5) can be eliminated since, it can get cancelled with the numerator
Hence, the removable discontinuity is at (x+5) or x= -5
Removable discontinuity is that which can be eliminated from the function.