Statement 1
the z-score of 194 lbs is
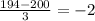
Reading the probability for z-score -2 on the table
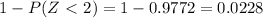
Then 0.0228×1000=23 spring that could withstand less than 194 lbs of force
Statement 2
The z-score of 194 lbs is -2
The z-score of 206 is
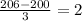
The probability between -2 and 2 is given by

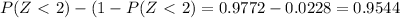
Then 0.9544×1000=954.4 springs could withstand the force between 194 lbs and 206 lbs
Statement 3
The z-score for 200lbs is 0, as it is the mean. The area to the right of z=0 is 0.5 which means half of 1000 springs could withstand the force more than 200lbs
Statement 4
The z-score of 206lbs is 2
The value of

Which is 0.0228×1000=22.8 springs could withstand more than 200 lbs of force
So the statement 1 is incorrect