Question

The average pulling force that a sample of 1000 springs could take and still be able to spring back was 200 lbs with a standard deviation of 3 lbs. If the distribution follows a normal curve, which of the following is NOT true?

A.) About 15 springs could withstand less than 194 lbs of force
B.) About 950 springs could withstand between 194 and 206 lbs of force.
C.) About 500 springs could withstand 200 lbs or more of force.
D.) About 25 springs could withstand more than 206 lbs of force.

Answer 1

Statement 1

the z-score of 194 lbs is
`(194-200)/(3) =-2`
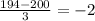
Reading the probability for z-score -2 on the table

`1-P(Z\ \textless \ 2)=1-0.9772=0.0228`
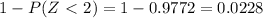
Then 0.0228×1000=23 spring that could withstand less than 194 lbs of force

Statement 2
The z-score of 194 lbs is -2
The z-score of 206 is
`(206-200)/(3) =2`
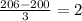
The probability between -2 and 2 is given by

`P(Z\ \textless \ 2)-P(Z\ \textless \ -2)`

`P(Z\ \textless \ 2)-(1-P(Z\ \textless \ 2)=0.9772-0.0228=0.9544`
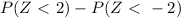
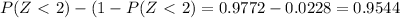
Then 0.9544×1000=954.4 springs could withstand the force between 194 lbs and 206 lbs

Statement 3

The z-score for 200lbs is 0, as it is the mean. The area to the right of z=0 is 0.5 which means half of 1000 springs could withstand the force more than 200lbs

Statement 4

The z-score of 206lbs is 2
The value of
`P(Z\ \textgreater \ 2)=1-P(Z\ \textless \ 2)=1-0.9772=0.0228`
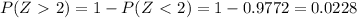
Which is 0.0228×1000=22.8 springs could withstand more than 200 lbs of force

So the statement 1 is incorrect