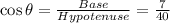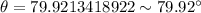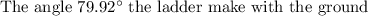Question

A ladder 40 feet in length rests against a vertical wall. The foot of the ladder is 7 feet from the wall. What angle, θ, does the ladder make with the ground? (Round angle measure to the nearest degree.)

Answer 1

`\text{The angle }79.92^(\circ) \text{ the ladder make with the ground}`

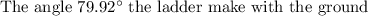
Step-by-step explanation

Given that a ladder 40 feet in length rests against a vertical wall. The foot of the ladder is 7 feet from the wall.

we have to find the angle θ the ladder make with the ground.

Length of ladder i.e AC=40 feet.

Distance of ladder from ground i.e BC=7 feet

By trigonometry formulas

`\cos \theta=(Base)/(Hypotenuse)=(7)/(40)`

`\theta = \cos^(-1)((7)/(40))`

`\theta=79.9213418922\sim 79.92^(\circ)`

`\text{The angle }79.92^(\circ) \text{ the ladder make with the ground}`

Answer 2

The ladder makes 79.92 degrees of angle with the ground (Calculation: Cos A = 7/40 = 0.175 resulting A = ACos 0.175 = 79.92 degrees). This problem can be solved by using a simple trigonometry formula of Cosine which stated Cos A = Adjacent/Hypotenuse. The ladder length of 40 feet is the hypotenuse side of the triangle and the 7 feet distance between the ladder's foot and the wall is the adjacent side.