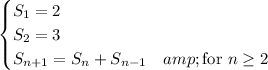Question

Given that S_n denotes the number of n-bit strings that do not contain the pattern 00, what is the recurrence relation?

Answer 1

There are two such possible strings, 0 and 1, so
`S_1=2`.

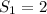
1 can be appended to either string, while 0 can only be appended to one, so
`S_2=3`.

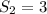
For an
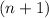
`(n+1)`-string to end with a 0, the bit in the
`n`th position needs to be a 1 - by definition, there are
`S_n` such possible strings.

If an
`n`-string already ends in a 0, we can drop this last bit to get an
`(n-1)`-string that ends in a 1 (we know this occurs because 00 is not allowed) - by definition there are
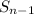
`S_(n-1)` such strings - and append 10 to it instead, giving an
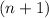
`(n+1)`-string that ends in a 0.

So, the number of
`n` bit strings not containing consecutive 0s is given recursively by


`\begin{cases}S_1=2\\S_2=3\\S_(n+1)=S_n+S_(n-1)&\text{for }n\ge2\end{cases}`