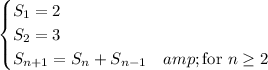There are two such possible strings, 0 and 1, so
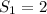
.
1 can be appended to either string, while 0 can only be appended to one, so
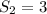
.
For an
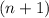
-string to end with a 0, the bit in the

th position needs to be a 1 - by definition, there are
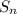
such possible strings.
If an

-string already ends in a 0, we can drop this last bit to get an

-string that ends in a 1 (we know this occurs because 00 is not allowed) - by definition there are
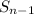
such strings - and append 10 to it instead, giving an
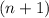
-string that ends in a 0.
So, the number of

bit strings not containing consecutive 0s is given recursively by