Question

If the legs of an isosceles right triangle have a length of 15√2 ft, the hypotenuse will have a length of _____feet.

Answer 1

The hypotenuse will have a length of __30___feet.

Explanation:

An isosceles right triangle:

It is a right triangle with two legs equal in length and has angles of
`45^(\circ)-45^(\circ)-90^(\circ)`

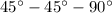
In a
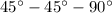`45^(\circ)-45^(\circ)-90^(\circ)` triangle,

the length of the hypotenuse is
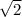`√(2)` times the length of a leg.

Given the statement:

If the legs of an isosceles right triangle have a length of 15√2 ft.

⇒Length of leg = 5√2 ft

then by definition we have;

`\text{Length of hypotenuse} = √(2) \cdot 15√(2)`

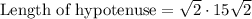
Simplify:

`\text{Length of hypotenuse} = 15 \cdot 2 = 30 ft`

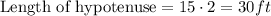
Therefore, the hypotenuse will have a length of __30___feet.

Answer 2

we know that

An isosceles triangle has two equal sides and two equal angles

If the isosceles triangle is a right triangle

then

The measure of the angles are
`45\°- 90\°- 45\°`

`cos (45\°)=(√(2))/(2)`

`cos (45\°)=(leg)/(hypotenuse)`

so

`(leg)/(hypotenuse)=(√(2))/(2)`

we have

`leg=15√(2)\ ft`

Substitute and solve for the hypotenuse

`(15√(2))/(hypotenuse)=(√(2))/(2)\\ \\hypotenuse=2*15 \\ \\ hypotenuse=30\ ft`

therefore

the answer is

`30\ feet`