Answer:
The hypotenuse will have a length of __30___feet.
Explanation:
An isosceles right triangle:
It is a right triangle with two legs equal in length and has angles of
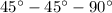
In a
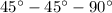 triangle,
triangle,
the length of the hypotenuse is
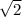 times the length of a leg.
times the length of a leg.
Given the statement:
If the legs of an isosceles right triangle have a length of 15√2 ft.
⇒Length of leg = 5√2 ft
then by definition we have;
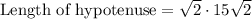
Simplify:
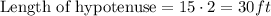
Therefore, the hypotenuse will have a length of __30___feet.