Question

Which is the graph of g(x)=(2/3)^x-2

Answer 1

Third graph

Explanation:

Answer 2

Graph has been shown in the attachments.

Explanation:

We have to graph the function
`y=\left((2)/(3)\right)^x-2`

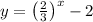
It represents an exponential function. Let us find the x and y intercepts,

For x-intercept, we plug y = 0

`0=\left((2)/(3)\right)^x-2`

`2=\left((2)/(3)\right)^x`

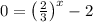
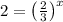
Take log both sides, we get

`\log 2=\log(\left((2)/(3)\right)^x)`

`x=-1.71`

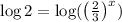
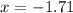
For y-intercept, we plug x=0

`y=\left((2)/(3)\right)^0-2`

`y=-2`

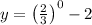
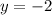
Therefore, the graph must passes through the points (0,-2) and (-1.71,0)

The horizontal asymptote of the graph is given by

`y=\lim_(x\rightarrow \infty )g(x)`

`y=\lim_(x\rightarrow \infty )\left((2)/(3)\right)^x-2`

`y=-2`

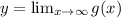
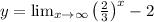
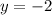
Hence, using these information, we can easily graph the function.