Answer:
Graph has been shown in the attachments.
Explanation:
We have to graph the function
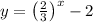
It represents an exponential function. Let us find the x and y intercepts,
For x-intercept, we plug y = 0
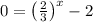
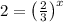
Take log both sides, we get
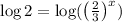
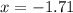
For y-intercept, we plug x=0
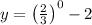
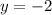
Therefore, the graph must passes through the points (0,-2) and (-1.71,0)
The horizontal asymptote of the graph is given by
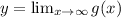
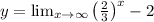
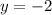
Hence, using these information, we can easily graph the function.