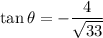Question

Find the value of tan θ for the angle shown. A line is drawn from the origin through the point square root of thirty-three comma negative four. The angle theta is given as the measurement from the positive x axis counterclockwise to the line.

Answer 1

If you draw this triangle on a graph as described, tan theta is -4(square root)33/33

Answer 2

The value of tan θ is:

`\tan \theta=-(4)/(√(33))`

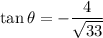
Explanation:

From the given right angled triangle we have:

Base of the triangle i.e. OA is: √33 units

and Perpendicular length of triangle i.e. AB is: 4 units

Hence, in the given right angled triangle we will use the trignometric ratio corresponding to the angle (360°-θ) as:

`\tan (360-\theta)=(perpendicular)/(base)\\\\\\\tan (360-\theta)=(4)/(√(33))`

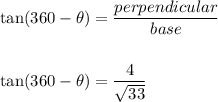
As we know that:

`\tan (360-\theta)=-\tan \theta`

Hence,

`-\tan \theta=(4)/(√(33))\\\\\\i.e.\\\\\\\tan \theta=-(4)/(√(33))`

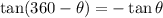
Hence, the answer is:

`\tan \theta=-(4)/(√(33))`