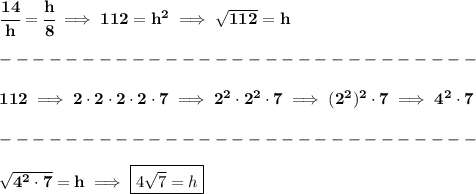Question

Use the diagram for questions 10 and 11

Answer 1

so hmmm notice the picture below

a perpendicular line, from the opposite side to the right-angle in a triangle, gives us, three similar triangles, a Large, containing the other two, a Medium, and a Small one

now, using proportions, let's say, "h" is the distance from the mall to home, and "p" the distance to the park


`\bf \cfrac{\textit{medium side}}{\textit{small side}}\qquad \cfrac{p}{6}=\cfrac{8}{p}\qquad \qquad \cfrac{\textit{large side}}{\textit{medium side}}\qquad \cfrac{14}{h}=\cfrac{h}{8}`




`\bf \cfrac{p}{6}=\cfrac{8}{p}\implies p^2=48\implies p=√(48)\\\\ -----------------------------\\\\ 48\implies 2\cdot 2\cdot 2\cdot 2\cdot 3\implies 2^2\cdot 2^2\cdot 3\implies (2^2)^2\cdot 3\implies 4^2\cdot 3\\\\ -----------------------------\\\\ p=√(4^2\cdot 3)\implies \boxed{p=4√(3)}`





`\bf \cfrac{14}{h}=\cfrac{h}{8}\implies 112=h^2\implies √(112)=h\\\\ -----------------------------\\\\ 112\implies 2\cdot 2\cdot 2\cdot 2\cdot 7\implies 2^2\cdot 2^2\cdot 7\implies (2^2)^2\cdot 7\implies 4^2\cdot 7\\\\ -----------------------------\\\\ √(4^2\cdot 7)=h\implies \boxed{4√(7)=h}`