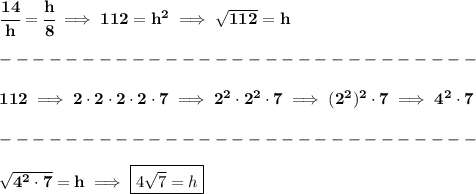so hmmm notice the picture below
a perpendicular line, from the opposite side to the right-angle in a triangle, gives us, three similar triangles, a Large, containing the other two, a Medium, and a Small one
now, using proportions, let's say, "h" is the distance from the mall to home, and "p" the distance to the park