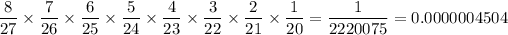Question

Solve the problem. eight basketball players are to be selected to play in a special game. the players will be selected from a list of 27 players. if the players are selected randomly, what is the probability that the 8 tallest players will be selected assuming none of the players are the exact same height

Answer 1

The probability is likely, because their are 27 players with 8 to chose from which leaves 19.

Answer 2

The probability is:

0.0000004504

Explanation:

We are given that:

eight basketball players are to be selected to play in a special game.

The players will be selected from a list of 27 players.

if the players are selected randomly.

We have to find the probability that the 8 tallest players will be selected assuming none of the players are the exact same height.

i.e. we need to select 8 members out of the 27 players no matter what the order is:

So, the probability is given as:

At the first place we have 8 choices out of 27.

so, the probability will be: 8/27.

at the second we have 7 choices out of 26 players.

( as 1 player has been chosen)

so, the probability is: 7/26

similarly for third choice the probability is: 6/25 and so on.

Hence, finally we get the probability as:

`(8)/(27)* (7)/(26)* (6)/(25)* (5)/(24)* (4)/(23)* (3)/(22)* (2)/(21)* (1)/(20)=(1)/(2220075)=0.0000004504`