Question

How many permutations exist of the letters PQRS and T taking four at a time

Answer 1

Looking at the permutation formula, we have n!/(n-r)!. n is the number of objects to select from and r is how many are to be picked at once. And 1 means multiply from there down basically. 5!/(5-4)!= 5*4*3*2*1/1. 5 times 4 is 20 times 3 is 60 times 2 is 120 times 1 is 1 so 120/1 is 120. There are 120 total combinations to be made from P, Q, R, S and T.

Answer 2

Answer: 120

Explanation:

The given letters : P Q R S T

Number of letters : 5

The formula of number of permutations of n things taken r at a time is given by :-

`^nP_r=(n!)/((n-r)!)`

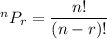
Similarly, the number of permutations of 5 letters taken four at a time is given by :-

`^5P_4=(5!)/((5-4)!)\\\\=(5!)/(1!)=5*4*3*2*1=120`

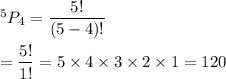
Hence, there are 120 permutations exists of the letters PQRS and T taking four at a time.