"Health Club A costs $2 more in monthly membership fees than Health Club B."
Let's compare the monthly membership fees of Health Club A and Health Club B based on the provided information.
For Health Club A, the equation seems to be linear. We can find the slope (m) and y-intercept (b) using the given points (x, y) from the table.
Let's use the points (11, 400) and (16, 575) to find the slope (m):
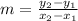
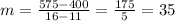
Now, we can use the slope and one point (let's use the point (11, 400)) to find the y-intercept (b) using the equation
y=mx+b:
400=35(11)+b
Solving for b:
b=400−35(11)=400−385=15
So, the equation for Health Club A is y=35x+15.
Now, let's compare the monthly membership fees of Health Club A and Health Club B:
Health Club A:
y=35x+15
Health Club B:
y=33x+45
Now, complete the sentence:
"Health Club A costs $ \underline{\hspace{2cm}} in monthly membership fees than Health Club B."
To fill in the blank, we need to subtract the corresponding coefficients of x in the two equations. In this case, it's 35−33, which equals 2. Therefore, the completed sentence is:
"Health Club A costs $2 more in monthly membership fees than Health Club B."